УДК 372.853                                                                                                                                                            А.В. Рябко

Використання інформаційних технологій у процесі дослідної перевірки правил Кірхгофа

У процесі виконання лабораторної роботи «Дослідна перевірка правил Кірхгофа» лабораторного практикума з курсу загальної фізики «Електрика і магнетизм» студенти розвивають практичні навички з розрахунку розгалуженого електричного кола за допомогою правил Кірхгофа.

Відомо, що закон Ома дає можливість проводити розрахунки тільки в простих електричних колах (наприклад, в одноконтурному колі). На практиці ж часто доводиться мати справу зі складними (розгалуженими) колами. Для спрощення розрахунків розгалужених кіл використовують правила Кірхгофа: 1)  алгебраїчна сума струмів, які сходяться у вузлі, дорівнює нулю

I₁ + I₂ + I₃…+ I_n= 0

Струми, що входять в вузол, і струми, що виходять з вузла, мають різні знаки.Напрям струму на кожній ділянці кола між двома вузлами можна вибирати довільно, зберігаючи цей напрям на всіх етапах роз’язування задачі. Якщо в результаті роз’язування для деяких струмів отримують від’ємні числові значення, то це означає, що початковий напрям цих струмів було вибрано неправильно.

2) у будь-якому замкненому контурі розгалуженого електричного кола алгебраїчна сума спадів напруг дорівнює алгебраїчній сумі електрорушійних сил, що діють в даному контурі

I₁R₁ + I₂R₂+ I₃R₃ +…+ I_nR_n= ε₁+ε₂ +ε₃ +…ε_n

Використовуючи правила Кірхгофа, розгалужене електричне коло постійного струму слід розрахувати в такій послідовності:

1. довільно вибрати напрям обходу контуру (за рухом стрілки годинника або проти);
2. довільно вибрати і позначити на схемі стрілками напрями струмів на всіх ділянках кола, при цьому в межах однієї ділянки (ділянка – це частина кола між сусідніми вузлами) струм повинен мати одне значення і напрям;
3. довільні замкнені контури обирають таким чином, щоб кожний новий контур мав хоча б одну ділянку кола, яка не входить до контурів, які вже обирали раніше;
4. якщо обраний напрям обходу контуру збігається з напрямом струму І_і, то добуток І_іR_i беруть із знаком плюс, якщо ж не збігається – то навпаки зі знаком мінус;
5. перед ЕРСε_і ставлять знак плюс, якщо при обході контуру доводиться йти усередині джерела від негативного до позитивного полюсу (тобто на шляху обходу контура потенціал зростає), у протилежному випадку ЕРС записують зі знаком мінус.

Правила Кірхгофа дають можливість визначити силу і напрям струму в будь-якій частині розгалуженого кола, якщо відомі опори його ділянок і ЕРС джерел струмів на цих ділянках.

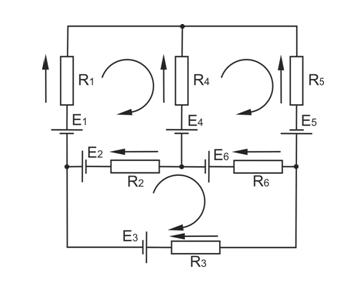
Наприклад, маємо коло, яке складається з декількох контурів, у кожному знаходиться джерело постійної ЕРС і резистор (рис.1). Необхідно розрахувати коло, тобто визначити силу струму у кожному контурі.Із законів Кірхгофа отримуємо систему рівнянь:

Розв’язок системи рівнянь часто може бути відносно громіздким і тривалим. Як і багато інших задач загального курсу фізики, ця задача може бути розв’язана за допомогою пакета MathCAD, який має потужній математичний апарат, що дозволяє розв’язувати системи алгебраїчних і диференціальних рівнянь, виконувати символьні обчислення, операції з векторами і матрицями, писати програми, будувати графіки і поверхні тощо.

Системи, які складаються на основі правил Кірхгофа, повністю визначаються своїми коефіцієнтами, які можна записати у вигляді матриць. Для того, щоб розв’язати систему рівнянь, які складаються на основі правил Кірхгофа, в документі MathCAD необхідно створити дві матриці. Перша (основна) матриця А повинна містити коефіцієнти при струмах, а друга В – праві частини рівнянь.Основна матриця даної системі лінійних рівнянь є квадратною і невиродженою, тому систему можна розв’язати матричним способом (за допомогою оберненої матриці). Щоб розв’язати систему у MathCAD використовуємо добуток матриці, яка обернена до основної, на другу матрицю: А^-1•В.

Для наведеного прикладу документ MathCAD має вигляд:

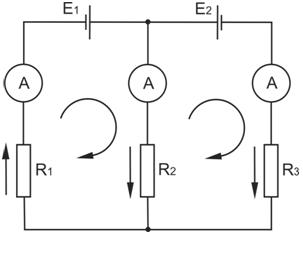
Для кола, яке використовується у даній лабораторній роботі (рис.2), система рівнянь для визначення невідомих струмів  I₁, I₂, I₃ має вигляд:

Документ MathCAD:

Файли зразків можна завантажити тут.

Список літератури

1. Майер Р.В. Решение физических задач с помощью пакета Mathcad / Р.В. Майер. – Глазов: ГГПИ, 2006. – 37 с.